Construir un sistema que aprenda ha sido tradicionalmente uno de los objetivos más escurridizos de la inteligencia artificial. El aprendizaje, es un proceso de adaptación al entorno; durante el se crean y manipulan representaciones que sean capaces de explicar dicho entorno.
En las redes neuronales la esencia del aprendizaje se encuentra en la modificación colectiva de los pesos de los elementos de procesado. Una definición de aprendizaje en redes neuronales podría ser la siguiente: Proceso por el cual los parámetros libres de una red neuronal son ajustados a través de un proceso continuo de estimulación por parte del entorno en donde se sitúa el sistema. El tipo de aprendizaje viene determinado por la forma en la que tienen lugar dichos cambios. Esta definición, implica tres hechos fundamentales:
- La red neuronal se encuentra estimulada por el entorno, cambia como consecuencia de esos estímulos y responde de manera diferente al entorno a causa de los cambios que se han producido en sus estructura interna.
Existen tres paradigmas de aprendizaje: Supervisado, No supervisado (o auto supervisado) y Reforzamiento (se puede considerar como un caso especial del aprendizaje supervisado).
Existen una gran cantidad variedad de algoritmos dentro de cada una de estas categorías.
En el aprendizaje supervisado (aprender con un maestro), la adaptación sucede cuando el sistema compara directamente la salida que proporciona la red con la salida que se desearía obtener de dicha red. Existen tres tipos básicos: por corrección de error, por refuerzo y estocástico.
En el aprendizaje por corrección de error el entrenamiento consiste en presentar al sistema un conjunto de pares de datos, representando la entrada y la salida deseada para dicha entrada (este conjunto recibe el nombre de conjunto de entrenamiento). El objetivo, es minimizar el error entre la salida deseada y la salida que se obtiene.
El aprendizaje por refuerzo, es más lento que el anterior. No se dispone de un ejemplo completo del comportamiento deseado pues no se conoce la salida deseada exacta para cada entrada sino que se conoce el comportamiento de manera general para diferentes entradas. La relación entrada-salida, se realiza a través de un proceso de éxito o fracaso, produciendo este una señal de refuerzo que mide el buen funcionamiento del sistema. La función del supervisor es más la de un crítico que la de un maestro.
El aprendizaje estocástico consiste básicamente en realizar cambios aleatorios de los valores de los pesos y evaluar su efecto a partir del objetivo deseado.
Supongamos que tenemos un conjunto de muestras de aprendizaje consistentes en vectores de entrada x y salidas deseadas d(x) (en tareas de clasificación d(x) es, usualmente, +1 o -1). La regla de aprendizaje del perceptrón es muy simple y se desarrolla a través de los siguientes pasos.
- 1. Iniciar la red con un conjunto aleatorio de pesos para las conexiones.
- 2. Seleccionar un vector de entrada x del conjunto de muestras de entrenamiento.
- 3. Si el perceptrón proporciona una salida incorrecta, modificar todas las conexiones mediante la expresión:
- 4. Volver al paso 2.
Cuando la red responde de forma correcta los pesos de las conexiones no se modifican.
Para una red con una única capa con un único elemento de procesado en la salida con una función de activación lineal, la salida viene dada por:
Una red simple con una única capa, es capaz de representar relaciones lineales entre el valor del elemento de procesado de la salida y el valor de los elementos de procesado de la entrada. Umbralizando el valor de la salida se puede construir un clasificador. Pero, también se pueden realizar otras tareas como aproximación de funciones. En espacios de entrada multidimensionales la red representa un hiperplano de decisión y es trivial asumir que se pueden definir varias unidades de salida.
Supongamos que vamos a entrenar una red para localizar el hiperplano de decisión más idóneo para un conjunto de muestras de entrada consistente en valores de entrada y valores de salida deseada . Para cada muestra dada del conjunto de entrada, la salida real de la red difiere de la salida deseada en , donde es la salida real para el patrón de entrada . La regla delta una función de error (o función de costo) basada en dicha diferencia para realizar el ajuste de los pesos.
La función de error, dada por el método del menor error cuadrático medio, es la suma de los cuadrados de los errores individuales de cada patrón. Es decir, el error total E viene dado por:
En donde el índice p recorre el conjunto de patrones de entrada y representa el error del patrón p-ésimo. Los valores de los pesos de conexión se buscan de forma tal que se minimice la función y este proceso se realiza por un método conocido gradiente descendiente. La idea del método, es realizar un cambio en los pesos inversamente proporcional a la derivada del error respecto al peso para cada patrón:
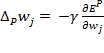
En donde ϒ es una constante de proporcionalidad. La derivada se puede descomponer mediante la siguiente expresión:
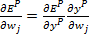
Dado que la función de activación es lineal, como se comentaba al comienzo,
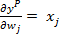
Y:
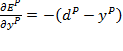
con lo cual:
En donde 
, es la diferencia entre la salida deseada y la salida real para el patrón de entrada p.
La regla Delta, modifica los pesos como función de las salidas deseada y real para unidades de entrada y salida binarias o continuas. Estas características abrieron un nuevo campo de posibilidades para las redes neuronales.
En donde:
Para realizar la generalización de la regla delta debemos considerar:
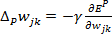
La medida de error Ep viene definida como el error cuadrático total para el patrón p en las unidades de salida N0.
Considerando E, como la suma de los errores cuadráticos podemos ver que la variación del error respecto a los pesos viene dada por:
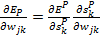
A partir de la expresión de la salida total y definiendo:
Se puede obtener una regla de actualización de pesos equivalente a la regla Delta, resultando un descenso en el valor del gradiente sobre la superficie de error si se realizan los cambios de los pesos de acuerdo a la expresión:
La conclusión más importante, es que el cálculo recursivo de los factores Delta puede implementarse propagando las señales de error desde la capa de salida a capas ocultas de la red.
El cálculo de 
puede realizarse en términos de un producto de dos factores; uno que refleje el cambio del error como función de la salida de las unidades y otro que refleje el cambio de la salida como función de los cambios en la entrada; es decir:
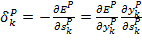
Ahora bien, el segundo factor no es otro que la derivada parcial de la función de activación F. Para calcular el primer factor vamos a considerar dos casos: que la unidad k es una unidad de salida de la red y que la unidad k es una unidad de una capa oculta.
En el primer caso, a partir de la definición del error para el patrón p, podemos obtener que:
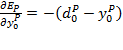
Que es el mismo resultado que en la regla Delta básica. Por tanto, para las unidades de la capa de salida:
En el segundo caso, no se conoce como contribuye la unidad al error de salida de la red, pero la medida de error se puede escribir como función de los pesos de las unidades de la capa oculta a la capa de salida:
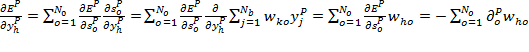
Con lo cual:
Extendiendo este cálculo de forma recursiva se pueden calcular los cambios en los pesos de todas las unidades de la red. Este procedimiento, se denomina regla Delta generalizada para redes feedforward con unidades no lineales.
En el aprendizaje no supervisado (o auto supervisado), la red se sintoniza a las regularidades estadísticas de datos de entrada de forma tal que se formen categorías que optimizan, respecto a los parámetros libres de la red, una medida de calidad de la tarea que se quiere realizar con la red. El funcionamiento de estas redes se basa en la búsqueda de características, regularidades, correlaciones y categorías del conjunto de datos de entrada.
Existen diferentes interpretaciones que se le pueden dar a las salidas generadas por una red que utilice este tipo de aprendizaje: similaridad (semejanzas entre la información actual y la información pasada), clusterización (establecimiento de clases), codificación (versión codificada de las entradas) o mapeo (representación topográfica de los datos de entrada).
El aprendizaje competitivo, es un proceso que divide el conjunto de patrones de entrada en clusters inherentes a los datos de entrada. El procedimiento de entrenamiento es muy simple: cuando se presenta un patrón de entrada se selecciona una única unidad de salida (la unidad ganadora) y se modifican los pesos de esa unidad.
Selección de la unidad ganadora mediante producto.
Asumamos que los patrones de entrada y los pesos están normalizados a la unidad. Cada unidad de salida o calcula su valor de activación a partir del producto del vector del patrón de entrada por el vector de pesos:
A continuación, se selecciona el elemento de procesado de salida que presenta mayor valor de activación. Su activación se pone a valor 1 y la del resto de elementos de procesado a 0. En este hecho radica el aspecto competitivo de la red.
Una vez que se ha seleccionado el elemento de procesado k ganador, se adaptan sus pesos (sólo del elemento ganador) de acuerdo a la expresión siguiente:
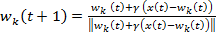
Cuando no se pueden utilizar patrones normalizados la elección del elemento de procesado ganador se realiza mediante el cálculo de la distancia Euclidiana entre el vector del patrón y el vector de pesos. Aquel vector de pesos que presente una distancia mínima determinará el elemento ganador. La ley de actualización de pesos del elemento ganador es la misma que en el caso anterior, sin el denominador pues los vectores no están normalizados.
En el aprendizaje con reforzamiento, la red aprende de relaciones entrada-salida. Sin embargo, al contrario que en el aprendizaje supervisado, el sistema conoce si la salida es correcta o no, pero no conoce la salida correcta.
ESCRIBIR UN COMENTARIO PARA EL PROXIMO CAPITULO
