Redes Neuronales Multicapa Con Aprendizaje Supervisado
La arquitectura de una red perceptrón consiste de una capa de S neuronas perceptrón, conectadas a r entradas a través de un conjunto de pesos Wij como se muestra en la figura 2.4. Como ya se mencionó anteriormente, los índices de la red i y j indican que Wij es la fuerza de conexión de la j-ésima entrada a la i-ésima neurona.
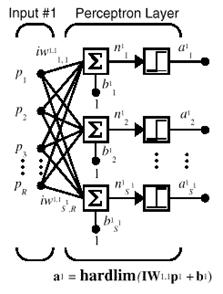
La red perceptrón puede tener únicamente una sola capa, debido a que la regla de aprendizaje del perceptrón es capaz de entrenar solamente una capa. Esta restricción coloca limitaciones en cuanto a lo que un perceptrón puede realizar computacionalmente.
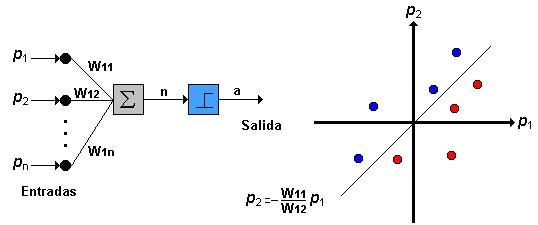
La única neurona de salida del Perceptrón realiza la suma ponderada de las entradas, resta el umbral y pasa el resultado a una función de transferencia de tipo escalón. La regla de decisión es responder +1 si el patrón presentado pertenece a la clase A, o –1 si el patrón pertenece a la clase B (figura 2.4), la salida depende de la entrada neta (n = en donde presenta la suma de las entradas pi ponderadas).
La red tipo Perceptrón emplea principalmente dos funciones de transferencia, función escalón (hardlim) con salidas 1, 0 o función escalón simétrica (hardlims) con salidas 1, -1; su uso depende del valor de salida que se espera para la red; es decir, sí la salida de la red es unipolar o bipolar; sin embargo, la función hardlims es preferida sobre la hardlim, ya que el tener un cero multiplicando algunas de los valores resultantes del producto de las entradas por el vector de pesos, ocasiona que estos no se actualicen y que el aprendizaje sea más lento.
Una técnica utilizada para analizar el comportamiento de redes como el Perceptrón es presentar en un mapa las regiones de decisión creadas en el espacio multidimensional de entradas de la red, en estas regiones se visualiza qué patrones pertenecen a una clase y cuáles a otra, el Perceptrón separa las regiones por un hiperplano cuya ecuación queda determinada por los pesos de las conexiones y el valor umbral de la función de activación de la neurona, en este caso los valores de los pesos pueden fijarse o adaptarse empleando diferentes algoritmos de entrenamiento.
Para ilustrar el proceso computacional del Perceptrón considere la matriz de pesos en forma general.
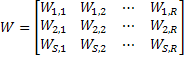
Los pesos para una neurona están representados por un vector compuesto de los elementos de la i-ésima fila de W:
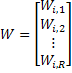
De esta forma y empleando la función de transferencia en escalón hardlim la salida de la neurona i de la capa de salida:
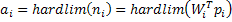
El Perceptrón, al constar de una sola capa de entrada y otra de salida con una única neurona, tiene una capacidad de representación bastante limitada, este modelo sólo es capaz de discriminar patrones muy sencillos, patrones linealmente separables (concepto que se estudiará en la sección 2.1.4), el caso más conocido es la imposibilidad del Perceptrón de representar la función OR EXCLUSIVA.


