Redes Neuronales Multicapa Con Aprendizaje Supervisado
1. Use un perceptrón simple para clasificar el siguiente conjunto de patrones:
a. Trace la frontera de decisión.
b. Encuentre la matriz de pesos W y el umbral de activación b .
c. Compruebe el funcionamiento del perceptrón con el conjunto de patrones de entrada
.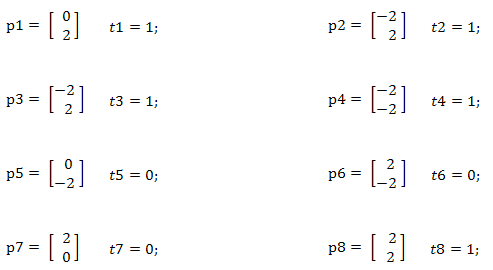
Se traza sobre la gráfica una línea que separe los patrones que arrojen salida 1 (negro) de los patrones cuya salida deseada sea 0 (Blanco). El trazo de esta línea o frontera de decisión depende del diseñador, siempre y cuando se cumpla la clasificación (separación de patrones con salida 1 de los de salida 0). El trazo de la frontera de decisión implica la determinación inmediata del vector de pesos que da solución al problema (la frontera de decisión es siempre perpendicular al vector de pesos W). Esto se muestra en la figura 2.6.
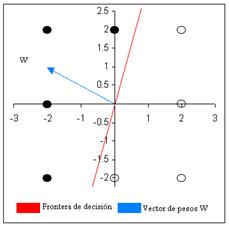
De la gráfica anterior, se obtiene el vector de pesos W:
W=[-2 1]
Dado que la frontera de decisión atraviesa por el origen (0,0), el umbral de activación es cero.
b=0
Para el primer par de entrada/salida
![]()
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el segundo par de entrada/salida
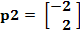
![]()
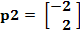
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el tercer par de entrada/salida
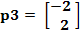
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el cuarto par de entrada/salida

![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el quinto par de entrada/salida
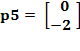
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el sexto par de entrada/salida
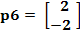
![]()
hola desde qui revisar
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el séptimo par de entrada/salida
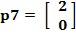
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el octavo par de entrada/salida
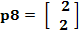
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
CONCLUSIÓN. Después de haber obtenido la matriz de pesos ![]() y el umbral
y el umbral ![]() que permiten clasificar los patrones mediante el método gráfico se concluye que el problema es linealmente separable y puede ser solucionado por un perceptrón simple, el cual introduce una sola frontera de decisión separado el espacio de los patrones en dos regiones.
que permiten clasificar los patrones mediante el método gráfico se concluye que el problema es linealmente separable y puede ser solucionado por un perceptrón simple, el cual introduce una sola frontera de decisión separado el espacio de los patrones en dos regiones.
- Resuelva el siguiente problema de clasificación del perceptrón y su regla de aprendizaje en donde los pares de entrada/salida son los siguientes:
- Usando la regla de aprendizaje del perceptrón, calcule la matriz de pesos
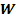 y el umbral de activación.
y el umbral de activación. - Grafique su solución, indicando la frontera la decisión y su vector de pesos.
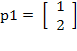
![]()
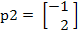
![]()
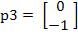
![]()
Solución
- Usando la regla de aprendizaje del perceptrón, calcule la matriz de pesos W y el umbral de activación b. Considere los parámetros iniciales:
![]()
![]()
![]()
Para el primer par de entrada/salida
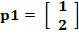
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Paso 3. Usando la regla de aprendizaje del perceptrón, se modifica el vector de pesos:
![]()
![]()
![]()
![]()
Paso 4. Para el umbral ![]() .
.
![]()
![]()
Para el segundo par de entrada/salida
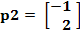
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red (Con los Nuevos Pesos):
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Paso 3. Usando la regla de aprendizaje del perceptrón, se modifica el vector de pesos:
![]()
![]()
![]()
![]()
Paso 4. Para el umbral ![]()
![]()
![]()
Para el tercer par de entrada/salida
![]()
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Paso 3. Usando la regla de aprendizaje del perceptrón, se modifica el vector de pesos:
![]()
![]()
![]()
![]()
Paso 4.Para el umbral ![]()
![]()
![]()
COMENTYARIO. Es necesario verificar, cuando se obtiene un vector de pesos nuevo que, el error e = 0 para todos los pares de entrada/salida, para dar por terminado el proceso de entrenamiento:
Para el primer par de entrada/salida
![]()
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el segundo par de entrada/salida
![]()
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Para el tercer par de entrada/salida
![]()
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Por lo tanto, los valores finales de ![]() y b son:
y b son:
W = [3 0.2]
b = 0
- Grafique su solución, indicando la frontera de decisión, y su vector de pesos.
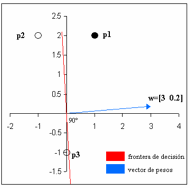
CONCLUSIÓN. La figura 2.7 muestra la solución del ejercicio. Donde se puede ver el vector de pesos W, la frontera de decisión (perpendicular al vector de pesos 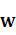 ) pasando por el origen, esto último se debe a que el valor del umbral b es cero.
) pasando por el origen, esto último se debe a que el valor del umbral b es cero.
Diseñe una red neuronal que permita clasificar dos tipos de fruta considerando la forma, la textura y el peso. Observe la figura 2.8.
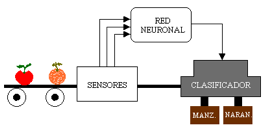
Figura 2.8: Clasificador De Frutas
Las entradas para el perceptrón tienen la forma siguiente:
P = 
Los valores para cada parámetro son:
Forma:
- 1, si la fruta es redonda.
- -1, si la fruta es elíptica.
Textura:
- 1, si la superficie de la fruta es suave.
- -1, si la superficie es rugosa.
Peso:
- 1,
 1 libra.
1 libra. - -1, < 1 libra.
Según lo anterior, los vectores de entrada para las frutas a clasificar son:
Naranja Manzana
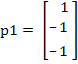
![]()

![]()
Considerando que los valores iniciales del vector de pesos y el umbral son:
![]()
![]()
- Aplique la regla de aprendizaje del perceptrón para calcular el vector de pesos W y el umbral b.
Solución
Primera época
Para el primer par de entrada/salida (Primera iteración)

![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
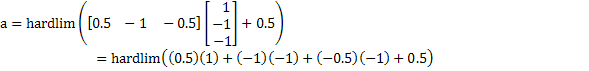
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Paso 3. Usando la regla de aprendizaje del perceptrón, se modifica el vector de pesos:
![]()
![]()
![]()
![]()
Paso 4. Para el umbral ![]()
![]()
![]()
Para el segundo par de entrada/salida (segunda iteración)
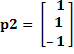
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
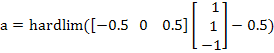
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Paso 3. Usando la regla de aprendizaje del perceptrón, se modifica el vector de pesos:
![]()
![]()
![]()
![]()
Paso 4. Para el umbral ![]()
![]()
![]()
Segunda época
Para el primer par de entrada/salida (Primera iteración)
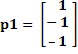
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()

![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Paso 3. Usando la regla de aprendizaje del perceptrón, se modifica el vector de pesos:
![]()
![]()
![]()
![]()
Paso 4. Para el umbral ![]()
![]()
![]()
Para el segundo par de entrada/salida (segunda iteración)
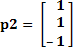
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
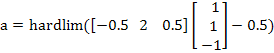
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
CONCLUSIÓN. De acuerdo a la regla de aprendizaje del perceptrón se ha alcanzado un mínimo por lo que se obtienen valores estables para la matriz de pesos 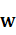 y el umbral
y el umbral 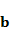 . Sólo resta comprobar si se cumple para el primer par de entrada
. Sólo resta comprobar si se cumple para el primer par de entrada  .
.
![]()
![]()
Paso 1. Se calcula la salida utilizando la función de activación propia de la red:
![]()
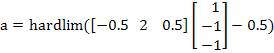
![]()
Paso 2. Se calcula el error:
![]()
![]()
![]()
Por lo tanto, los valores finales de W y b son:
![]()
![]()


