Funciones Lineales Importantes en MATLAB

Las redes lineales pueden inicializarse, diseñarse y simularse con tres funciones: initlin, solvelin y simulin. La función de simulación simulin usa la función de transferencia purelin, usada por las redes lineales. Las redes lineales off-line, se pueden entrenar con la función trainwh, y adaptablemente con la función adaptwh.

Teclee help linnet para obtener una lista de funciones de las redes lineales, además de demostraciones y aplicaciones.

Fundamentos. Modelo de la Neurona

Una neurona lineal con entradas R se muestra en la Fig. 2.24.

Note que la neurona lineal usa la función de transferencia purelin. La función de transferencia lineal purelin calcula la salida  de la neurona devolviendo el valor pasado a ella simplemente. Las siguientes dos líneas de código (Para una Capa de Neuronas) son equivalentes.

	( 2 . 30 )
	( 2 . 31 )

Cuando se está presentando una matriz de entradas a una capa con más de una neurona y umbrales, debe llamarse a la función purelin con el umbral como un segundo argumento.

( 2 . 32 )

Alternativamente, la función de simulación lineal simulin pueden usarse  para calcular la salida como que pueden llamarse a la función como sigue:

( 2 . 33 )

Al igual que con el Perceptrón, los umbrales son útiles, como parámetros de la red porque ellos proporcionan una variable libre adicional que puede ajustarse para obtener la actuación deseada de la red. A la neurona lineal se le puede entrenar para aprender una función de su entrada, o para encontrar una aproximación lineal de una función  no lineal. Una red lineal no puede, por supuesto, desempeñar un cálculo no lineal.

Inicialización

La función initlin, se usa para inicializar los pesos y umbrales de la capa lineal a valores iniciales  positivos y negativos pequeños. El código de la inicialización para una capa de siete neuronas lineales de cinco entradas sería:

( 2 . 34 )

Sean las matrices de P vectores de entrada y T vectores objetivo, están disponibles. La función initlin puede inferir el número de neuronas de entrada basándose en el número de filas de P y T.

( 2 . 35 )

Diseño

A diferencia de las otras arquitecturas de redes neuronales, las redes lineales se pueden diseñar directamente si todos los pares de vectores entrada/salida son conocidos. Dado este caso la función solvelin se puede usar para encontrar los valores de pesos y umbrales (  y ) sin entrenamiento.

( 2 . 36 )

Si se llama a la función solvelin con dos  argumentos de salida, esta diseña una red con pesos y umbrales. Si se llama a la función con un solo argumento  la función diseñara una red con la matriz de pesos  pero sin ningún umbral. En cada caso la solución del mínimo error cuadrático se encuentra. Se usan los umbrales  porque una red con umbrales nunca tiene un  error mayor que la misma red sin umbrales, y a menudo tiene el más bajo error.

( 2 . 37 )

Si existe una solución de cero-error, esta será  encontrará por la función solvelin.

Si ninguna solución lineal perfecta existe se devolverán los valores representando a la red con el mínimo error cuadrático sumado sse. Si hay más de una solución de cero-error, solvelin devuelve la solución con los pesos y umbrales más pequeños.

La sección siguiente describe cómo entrenar una red lineal para encontrar una solución. ¿Por qué entrenar una red en lugar de usar la función solvelin?. Primero, a veces la función solvelin no pueden resolver directamente los pesos y umbrales de la red. Se puede llamar a solvelin y ver el siguiente mensaje: Warning: Matriz is singular to working precision (La matriz es singular a la precisión activa)

Cuando los cálculos realizados por solvelin no son numéricamente estables, todavía se puede entrenar la red lineal con las funciones learnwh y trainwh a una aproximación de la solución ideal.

Regla de Aprendizaje

Las redes lineales son entrenadas con ejemplos de conducta correcta. La regla de Widrow-Hoff  mediante la función learnwh, calcula los cambios a los pesos y umbrales de una capa lineal disminuyendo la suma de errores cuadrados de la capa. La función learnwh toma como  argumentos el vector de entrada P presentado a la red, y el error de la red E (la diferencia entre la salida de la red A y un objetivo T designado).

( 2 . 38 )

Un argumento adicional, la proporción de aprendizaje lr, actúa como una ganancia en el cambio de los pesos y los umbrales. Si el parámetro lr es grande, el aprendizaje ocurre rápidamente, pero si el aprendizaje es demasiado grande, puede hacerse inestable y los errores incluso pueden aumentar.

Para asegurar el aprendizaje estable, la velocidad de aprendizaje lr debe ser menor al recíproco del eigenvector más grande de producto de la matriz P'*P. La función maxlinlr calcula la proporción máxima de aprendizaje estable (0.999 * P'*P).

                              % si ningún umbral se usa.

)      % si usan los umbrales.

Así, una vez que la proporción de aprendizaje es calculada, las líneas siguientes de código reducirán el error de la red asociado con las matrices de entrada y vectores objetivo, P y T, con cada iteración.

 

 

 

 

;

La regla de Widrow-Hoff calcula los cambios pequeños para los pesos de una neurona y umbrales en la dirección que disminuye el error de la neurona. Esta dirección se encuentra tomando la derivada del error cuadrado sumado sse con respecto a estos parámetros

Entrenamiento

La función trainwh aplica repetidamente las entradas p a una red lineal con la función  simulin y calcula los errores con respecto a los vectores objetivo T, y encuentra los nuevos pesos y umbrales. Se repite este ciclo hasta que el error cuadrático sumado  cae bajo un valor meta, o bien  se cumple un número máximo de épocas.

Los cuatro parámetros de entrenamiento tp, determinan qué tan a menudo ocurre el progreso en mostrar resultados, el número máximo de épocas para entrenar, la meta del error deseada, y la razón de aprendizaje. Cualquiera o todos estos parámetros se pueden ajustarse a un valor de NaN. Además, los parámetros tp pueden contener una lista parcial de valores, ningún valor o simplemente no ser pasados a trainwh. Los valores indefinidos y los parametros NAN serán puestos a sus valores predefinidos. Se puede ver estos valores predefinidos tecleando help trainwh. Además, de regresar los valores de los nuevos  pesos W y umbrales  b, la función trainwh devuelve el número de épocas que realmente ocurrieron ep, y un registro de los errores a lo largo del entrenamiento tr.

Ejemplo 1:

1.      Resuelva el siguiente problema de clasificación de la red Adaline y su regla de aprendizaje

Los pares de entrada/salida son:

        

        

     

En el editor de Matlab teclee el siguiente código que resuelve el problema anterior:

En la ventana de comandos de Matlab aparece paso a paso la ejecución del programa, como sigue:

 

La salida del programa (Además, del Proceso Descrito en la Ventana de Comandos de Matlab) es una sucesión de gráficas donde aparece la variación del error en un número N de épocas. Esto se muestra en la Fig. 2.25.

 

 

 

 

 

 

 

Fig. 2.25.

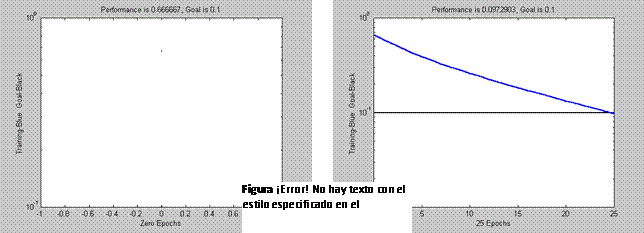Los patrones de entrada en un plano de dos dimensiones, con la clasificación correspondiente (Frontera de Decisión) aparecen después de terminado el proceso de entrenamiento. Esto se muestra en la Fig. 2.26.

 

 

 

 

 

 

Fig. 2.26.

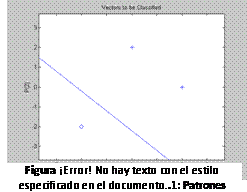Ejemplo 2: Predicción Adaptativa con Adaline –(adlpr.m)

 

En este ejemplo una configuración Adaline es usada para predecir una señal de unidimensional (Series de Tiempo). Para predecir el siguiente valor de la señal de entrada, p muestras de ésta son colocados a la Adaline. La señal de entrada es también usada como la salida deseada. La regla de aprendizaje LMS es usada para adaptar el vector de pesos en cada paso.

 

Empezaremos con las especificaciones de una señal senoidal de frecuencia 2kHz muestreada cada 50msec. Después de 5sec la frecuencia de la señal se cuadruplicará con el tiempo de muestreado siendo también reducido a 12.5msec.

 

 

 

 

 

 

 

 

 

 

 

 

 

Figura 2 .27: La Señal de Entrada y la Señal Predicha

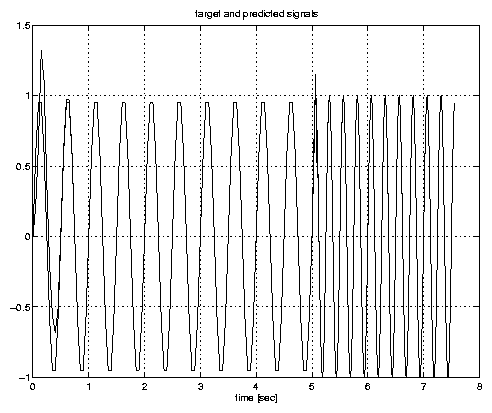
La señal (Series de Tiempo) se convertirá en una colección de vectores de entrada,  y guardadas en una matriz de .

 

El vector de pesos estimado es

NOTA: