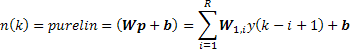Redes Neuronales Multicapa Con Aprendizaje Supervisado
Esta red ha sido extensamente utilizada en ciencia, estadística (En el Análisis de Regresión Lineal), ingeniería (El Procesamiento Adaptativo de Señales, Control de Sistemas), y así sucesivamente.
En general, la Adaline es usada para ejecutar:
- Una aproximación lineal de un pequeño segmento de una superficie no lineal, la cual es generada por una función variable , En este caso, el bias es usualmente necesario, de aquí, wp=1 .
- Filtrado lineal de datos (señales).
- Asociación de patrones, esto es, generación de m-elemento del vector de salida asociados con su respectivo p-elemento del vector de entrada.
La red Adaline ha sido ampliamente utilizada en el procesamiento de señales; para valorar el real aporte de esta red en ese campo, se detallarán un poco las herramientas hasta ahora empleadas en los procesos de filtrado.
A comienzos del estudio de las comunicaciones electrónicas, se diseñaban filtros analógicos empleando circuitos RLC (Resistencias, Inductores, Condensadores) para eliminar el ruido en las señales empleadas de comunicaciones; este procesamiento se ha transformado en una técnica de múltiples facetas, destacándose en la actualidad el uso de procesadores digitales de señales (DSP), que pueden llevar a cabo los mismos tipos de aplicaciones de filtrado ejecutando filtros de convolución realizados mediante programación convencional, en cualquier lenguaje de programación conocido.
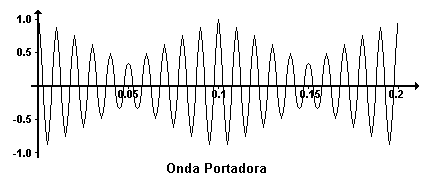
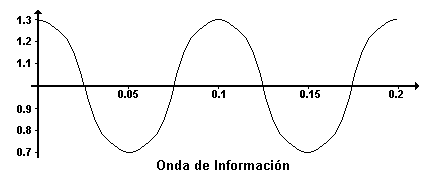
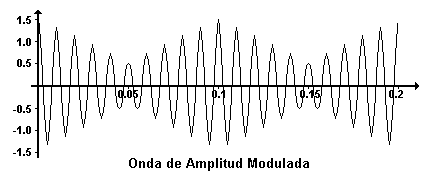
El proceso de filtrado sigue ocupando un lugar muy importante en la industria, pues siempre será necesario eliminar el ruido en señales portadoras de información. Considérese una transmisión de radio en AM, las técnicas electrónicas de comunicación, bien sean para señales de audio o de datos constan de una codificación y una modulación de la señal. La información que hay que transmitir, se puede codificar en forma de una señal analógica que reproduce exactamente las frecuencias y las amplitudes del sonido original. Dado que los sonidos que se están codificando representan un valor continuo que va desde el silencio, pasando por la voz, hasta la música, la frecuencia instantánea de la señal variará con el tiempo, oscilando entre 0 y 10,000 Hz aproximadamente.
En lugar de intentar transmitir directamente esta señal codificada, se transmite la señal en forma más adecuada para la transmisión por radio; esto se logra modulando la amplitud de una señal portadora de alta frecuencia con la señal de información analógica. Para la radio AM, la frecuencia portadora estará en el intervalo de los 550 a los 1650 kHz , dado que la frecuencia de la portadora es muy superior a la frecuencia máxima de la señal de información, se pierde muy poca información como consecuencia de la modulación; la señal modulada puede ser transmitida después a una estación receptora (o se puede retransmitir a cualquiera que tenga un receptor de radio), en la cual la señal se demodula y se reproduce en forma de sonido.
La razón más evidente para utilizar un filtro en una radio de AM es que cada persona tiene sus preferencias de música y diversión y dado que hay tantas emisoras de radio diferentes es necesario permitir que cada usuario sintonice su receptor a una cierta frecuencia seleccionable. Al sintonizar la radio, lo que se esta haciendo es, modificar las características de respuesta en frecuencia de un filtro pasa banda que está dentro de la radio, este filtro solo deja pasar las señales procedentes de la emisora en la que se este interesado y elimina todas las demás señales que estén siendo transmitidas dentro del espectro AM.
La herramienta matemática para el diseño de filtros más utilizada es la Serie de Fourier, que describe la naturaleza de las señales periódicas en el dominio frecuencial y está definida como:

En donde:
f0: Frecuencia fundamental de la señal en el dominio del tiempo.
an y bn: Coeficientes necesarios para modular la amplitud de los términos individuales de la serie.
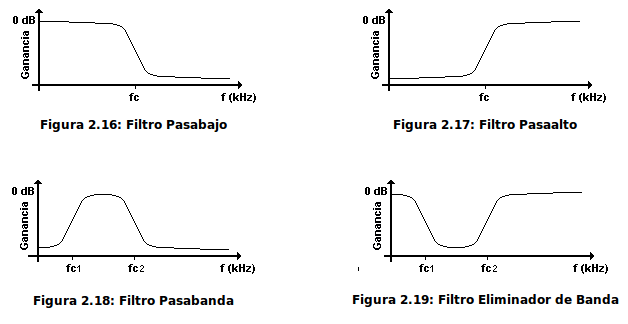
Las primeras realizaciones de los cuatro filtros básicos de las siguientes figuras poseían una gran limitación: Solo eran ajustables en un pequeño intervalo.
Todos los filtros se pueden caracterizar a partir de su respuesta a la función de impulso unitario, que se representa por δ(n) en la forma:
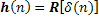
La ventaja de esta formulación es que una vez se conoce la respuesta del sistema para el impulso unitario, la salida del sistema para cualquier entrada está dada por:
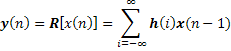
En donde x(n) es la entrada al sistema.
Esta ecuación describe una convolución entre la señal de entrada y la respuesta del sistema al impulso unitario. Para este caso, basta tener en cuenta que la convolución es una operación de suma entre productos, similar al tipo de operación que realiza un Perceptrón cuando calcula su señal de activación. La red Adaline emplea este mismo cálculo para determinar cuanta estimulación de entrada recibe a partir de una señal instantánea de entrada; esta red tiene diseñado en su interior una forma de adaptar los coeficientes ponderables (pesos de la red) para hacer aumentar o disminuir la estimulación que recibirá la próxima vez que se le presente la misma señal. La utilidad de esta capacidad se pone de manifiesto cuando se diseña un filtro digital por medio de software; con un programa normal, el programador debe saber exactamente como se específica el algoritmo de filtrado y cuales son los detalles de las características de las señales; si se necesitaran modificaciones, o si cambian las características de la señal, es necesario reprogramar; cuando se emplea una red tipo Adaline, el problema se convierte, en que la red sea capaz de especificar la señal de salida deseada, dada una señal de entrada específica.
La red Adaline toma la entrada y la salida deseada, y se ajusta a sí misma para ser capaz de llevar a cabo la transformación deseada. Además, si cambian las características de la señal, la red Adaline puede adaptarse automáticamente.
En orden a usar la red tipo Adaline para implementar un filtro adaptivo, se debe incorporar el concepto de retardos en línea, el cual se visualiza en la Fig. 2.20:
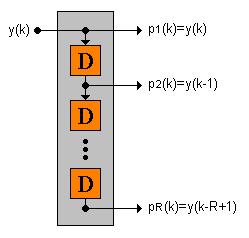
Si se combina la red Adaline con un bloque de retardos en línea, se ha creado un filtro adaptable como el de la Fig 2.21.
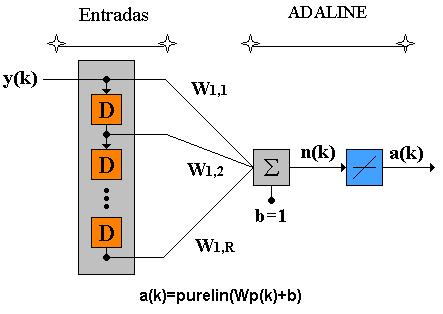
Cuya salida está dada por: