En las redes con aprendizaje competitivo (Y Cooperativo), suele decirse que las neuronas compiten (Y Cooperan) unas con otras con el fin de llevar a cabo una tarea dada. Con este tipo de aprendizaje se pretende que cuando se presente a la red cierta información de entrada, sólo una de las neuronas de salida de la red, o una por cierto grupo de neuronas, se active (Alcance su Valor de Respuesta Máximo). Por tanto las neuronas compiten para activarse quedando finalmente una, o una por grupo, como neurona vencedora y el resto quedan anuladas y siendo forzadas a sus valores de respuesta mínimos.

La competición entre neuronas se realiza en todas las capas de la red, existiendo en estas redes neuronas con conexiones de autoexitación (Signo Positivo) y conexiones de inhibición (Signo Negativo) por parte de neuronas vecinas.

El objetivo de este aprendizaje es categorizar (Clusterizar) los datos que se introducen en la red, de esta forma las informaciones similares son clasificadas formando parte de la misma categoría y por tanto deben activar la misma neurona de salida. Las clases o categorías deben ser creadas por la propia red, puesto que se trata de un aprendizaje no supervisado a través de las correlaciones entre los datos de entrada.

A principios de 1959, Frank Rosenblatt creó su simple clasificador espontáneo, una red de aprendizaje no supervisado basado en el Perceptrón, el cual aprendía a clasificar vectores de entrada en dos clases con igual número de términos.

A finales de los años 60’s y principios de los 70’s, Stephen Grossberg introdujo muchas redes competitivas que usaban inhibición lateral obteniendo buenos resultados. Algunos de los comportamientos útiles obtenidos por él, fueron la supresión del ruido, aumento del contraste y normalización de vectores.

En 1973, Christoph Von Der Malsburg introduce la regla del mapa de organización propia, que permitía a la red clasificar entradas en las cuales las neuronas que estuviesen en un vecindario cercano a la neurona ganadora, respondieran a entradas similares. La topología de esta red imitaba de alguna forma las estructuras encontradas en la corteza visual de los gatos, estudiada por David Hubel y Torten Wiesel. Su regla de aprendizaje generó gran interés, pero esta utilizaba un cálculo no local para garantizar que los pesos fueran normalizados, este hecho hacía este modelo biológicamente poco posible.

Grossberg extendió el trabajo de Von Der Malsburg, redescubriendo la regla Instar. Grossberg mostró que la regla Instar removió la necesidad de renormalizar los pesos, porque los vectores de pesos que aprendían a reconocer vectores de entrada normalizados, automáticamente se normalizarán ellos mismos.

El trabajo de Grossberg y Von Der Malsburg enfatizó la posibilidad biológica de sus redes. Otro exitoso investigador, Tuevo Kohonen ha sido también un fuerte proponente de las redes competitivas; sin embargo, su énfasis ha sido en aplicaciones para ingeniería y en descripciones de eficiencia matemática de las redes. Durante la década de los 70 Kohonen desarrolló una versión simplificada de la regla Instar, inspirada también en la red de Von Der Malsburg y Grossberg, de esta forma encontró una manera muy eficiente de incorporar topología a una red competitiva.

Otra forma de aplicar este tipo de aprendizaje fue propuesta por Rumelhart y Zisper [32] en 1985, quienes utilizaban redes multicapa dividiendo cada capa en grupos de neuronas, de tal forma que éstas disponían de conexiones inhibitorias con otras neuronas de su mismo grupo y conexiones excitadoras con las neuronas de la siguiente capa; en una red de este tipo, después de recibir diferentes informaciones de entrada, cada neurona en cada grupo se especializa en la respuesta a determinadas características de los datos de entrada.

En este tipo de redes cada neurona tiene asignado un peso total (Suma de Todos los Pesos de las Conexiones que Tiene a su Entrada), el aprendizaje afecta sólo a las neuronas ganadoras (Activas), en las que se redistribuye el peso total entre sus conexiones y se sustrae una porción de los pesos de todas las conexiones que llegan a la neurona vencedora, repartiendo esta cantidad por igual entre todas las conexiones procedentes de unidades activas, por tanto la variación del peso de una conexión entre una unidad i y otra j será nula si la neurona j no recibe excitación por parte de la neurona i (No Vence en Presencia de un Estímulo por Parte de i) y se modificará (Se Reforzará) si es excitada por dicha neurona.

Una variación del aprendizaje supervisado aplicado a redes multicapa consiste en imponer una inhibición mutua entre neuronas únicamente cuando están a cierta distancia unas de otras (Suponiendo que las Neuronas se han Dispuesto Geométricamente, por Ejemplo Formando Capas Bidimendisionales), existe entonces un área o región de vecindad alrededor de las neuronas que constituye un grupo local.

Fukushima [11] empleó esta idea en 1975 para una red multicapa llamada Cognitron, fuertemente inspirada en la anatomía y fisiología del sistema visual humano y en 1980 el mismo Fukushima [12] en una versión mejorada de la anterior a la que llamó Necognitron, presentó una variación de esta red utilizando aprendizaje supervisado. El Necognitrron disponía de un gran número de capas con arquitectura muy específica de interconexiones entre ellas y era capaz de aprender a diferenciar caracteres, aunque estos se presentasen a diferente escala, en diferente posición o distorsionados.

El aspecto geométrico de la disposición de neuronas de una red, es la base de un caso particular de aprendizaje competitivo introducido por Kohonen en 1982 conocido como feature mapping (Mapas de Características), aplicado en redes con una disposición bidimensional de las neuronas de salida, que permiten obtener mapas topológicos o topográficos (Topology Preserving Maps, Topographics Maps, Self Organization Maps) en los que de algún modo estarían representadas las características principales de las informaciones presentadas a la red. De esta forma, si la red recibe informaciones con características similares, se generarían mapas parecidos, puesto que serían afectadas neuronas de salidas próximas entre sí.

Estructura General de una Red Competitiva

En las redes asociativas, se vio como la regla instar puede aprender a responder a un cierto grupo de vectores de entrada que están concentrados en una región del espacio. Supóngase que se tienen varias instar agrupadas en una capa, tal como se muestra en la figura siguiente, cada una de las cuales responde en forma máxima a un cierto grupo de vectores de entrada de una región distinta del espacio.

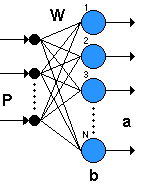
Figura 4.2: Instar Agrupadas en una Capa

Se puede decir que esta capa de Instars clasifica cualquier vector de entrada, porque la Instar con la mayor respuesta para alguna entrada dada es la que identifica a la región del espacio en la cual yace el vector de entrada. En lugar de examinar la respuesta de cada instar para determinar cuál es la mayor, la labor de clasificación sería más fácil si la Instar de mayor respuesta fuera la única unidad que tuviese una salida no nula; esto se puede conseguir si las instar compiten unas con otras por el privilegio de la activación, este es el principio de las redes competitivas.

Problemas Con Las Redes De Aprendizaje Competitivo

Las redes competitivas, son bastante eficientes para resolver problemas de clasificación, sin embargo presentan algunos problemas. El primero es la elección de una rata de aprendizaje que permita hallar un punto de equilibrio entre velocidad de convergencia y la estabilidad final de los vectores de peso. Una rata de aprendizaje cercana a cero, torna el aprendizaje muy lento pero garantiza que cuando un vector haya alcanzado el centro de la clase objetivo, se mantendrá allí indefinidamente. En contraste, una rata de aprendizaje cercana a uno genera un aprendizaje muy rápido, pero los vectores de peso continuarán oscilando aún después de que se haya alcanzado convergencia. La indecisión que se presenta al escoger la rata de aprendizaje puede ser empleada como una ventaja si se inicia el entrenamiento con una rata de aprendizaje alta y se decrementa en el transcurso del proceso de entrenamiento cuando sea necesario, desafortunadamente esta técnica no funciona si la red necesita continuamente ser adaptada a nuevos argumentos de los vectores de entrada (Caso en que la Red se Trabaje On-Line).

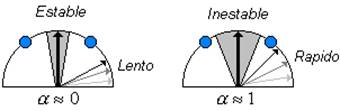
Figura 4.3: Variación de la rata de aprendizaje

Un problema de estabilidad más serio, ocurre cuando las clases están muy juntas; en ciertos casos, un vector de pesos tratando de apuntar hacia una clase determinada, puede entrar al territorio de otro vector de pesos. En la figura anterior, pueden observarse con círculos azules, como dos vectores de entrada son presentados repetidas veces a la red; el resultado, es que los vectores de pesos que representan las clases de la mitad y de la derecha se encuentran a la derecha. Con seguridad, se presentará el caso en que una de las clases de la derecha será clasificada por el vector de pesos del centro.

Figura 4.4: Aprendizaje Inestable

Un tercer problema con redes competitivas, es que es posible que el vector de pesos inicial de una neurona se encuentre muy lejos de cualquiera de los vectores de entrada y por lo tanto nunca gane la competición. La consecuencia será, la "muerte" de la neurona, lo que por supuesto no es recomendable.

Figura 4.5: Causa de la Muerte de una Neurona

En la figura anterior el vector de peso w3 nunca ganará la competición, sin importar cual sea el orden en que se le presenten los vectores de entrada. Una solución a este problema, consiste en adicionar una ganancia negativa a la entrada neta de cada neurona y decrementar así la ganancia total cada vez que la neurona gane la competición; esto hará que difícilmente una neurona gane varias veces la competición, a este mecanismo se le llama "conciencia".

Una capa competitiva tiene tantas clases como neuronas, lo que podría complicar algunas aplicaciones, especialmente cuando el número de clases no se conoce de antemano. En capas competitivas, cada clase consiste de una región convexa del espacio de entrada, las capas competitivas no pueden formar clases con regiones no convexas o clases que sean la unión de regiones no conectadas.