En este punto es posible diseñar una red competitiva que realice clasificaciones correctas fijando el valor de las filas de W en los valores del vector prototipo esperado, sin embargo es deseable tener una regla de aprendizaje que pueda entrenar los pesos en una red competitiva sin conocer los vectores prototipo, una de estas reglas es la Instar:

	(4.18)

Para redes competitivas, a tiene un valor diferente de cero solamente para la neurona ganadora (i=i*), de esta forma los mismos resultados serán obtenidos utilizando la regla de Kohonen.

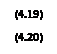Así, la fila de la matriz de pesos que esté más cerca al vector de entrada (O Tenga el Producto Punto más Grande con el Vector de Entrada) se moverá hacía el vector de entrada. Este se mueve a lo largo de la línea entre la fila anterior del vector de pesos y el vector de entrada, como puede verse en la Figura 4.8.

Figura 4.8: Representación Gráfica de la Regla de Kohonen

Para demostrar cómo trabaja una red competitiva, se creará una red que clasifique los siguientes vectores:

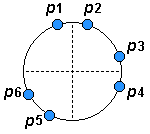
Figura 4.9: Vectores de Entrada

La red tendrá tres neuronas, por lo tanto los vectores serán clasificados en tres clases o grupos, esta es una de las principales características de las redes competitivas, ellas pueden agrupar los patrones de entrada en clases que no se conocen. Los pesos normalizados escogidos aleatoriamente son:

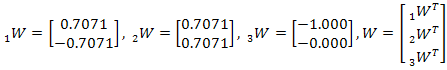
Los vectores de datos y los pesos asignados pueden visualizarse en la Figura 4.10:

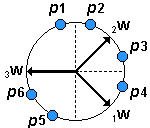
Figura 4.10: Vectores de Entrada y Vectores de Pesos

Se presenta a la red el vector

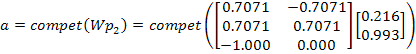
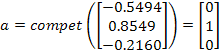
El vector de peso de la segunda neurona estaba más cercano a , por lo tanto ganó la competición (i*=2) y su salida es 1. Ahora se aplicará la regla de Kohonen a la neurona ganadora con una rata de aprendizaje .

La regla de Kohonen hace que  tienda hacia  como puede verse en la Figura 4.11, si continuamos escogiendo vectores de entrada aleatoriamente y presentándoselos a la red, en cada iteración el vector de pesos se acercará más al vector de entrada.

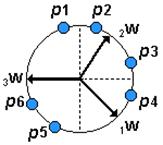
Figura 4.11: Proceso de Entrenamiento

Cada vector de pesos apuntará hacia una clase diferente del vector de entrada, convirtiéndose en un prototipo para esa clase. Cuando termine el proceso de entrenamiento, los pesos finales se verán como aparece en la Figura 4.12:

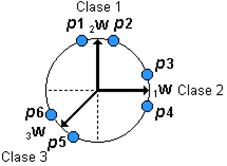
Figura 4.12: Pesos Finales