A. Funcionamiento.

Se trata de una red auto asociativa. Por tanto, informaciones diferentes (patrones) pueden ser almacenadas en la red, como si de una memoria se tratase, durante la etapa de aprendizaje. Posteriormente, cuando se presenta una entrada a la red, esta evoluciona hasta generar una salida que coincidirá con la que corresponde a esa entrada, o bien la más parecida si la entrada está distorsionada o incompleta.

La información que recibe la red debe haber sido previamente codificada y representada en forma de vector (como una configuración binaria o como un conjunto de valores reales dependiendo de si la red es discreta o continua) con tantas componentes como neuronas (N) tenga la red. Cada neurona recibe un elemento del vector.

Centrándonos en una sola neurona el funcionamiento sería el siguiente:

• Recibe como entrada la salida de cada una de las otras neuronas (por las conexiones laterales) Estos valores de salida, inicialmente coinciden con las entradas del vector, multiplicadas por los pesos de las conexiones correspondientes. La suma de todos estos valores constituirá el valor de entrada neta de la neurona a la que hay que aplicarle la función de transferencia obteniéndose el valor de salida correspondiente. En el instante inicial () la información de entrada es ()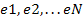

(5.26)

(5.27)

(5.28)

• Este proceso continúa hasta que las salidas de las neuronas se estabilizan, alcanzan la convergencia, durante algunas iteraciones.

(5.29)

La red Hopfield continua, con funciones de activación de tipo sigmoidal, ofrece más posibilidades que la discreta ya que permite almacenar patrones formados por valores reales (por ejemplo, imágenes en color o en blanco y negro con diferentes tonalidades de grises).

Otro aspecto importante en el funcionamiento de la red es el instante en que se produce la generación o actualización de las salidas. Si la actualización se realiza de forma simultánea en todas las neuronas el funcionamiento es paralelo o síncrono. Si, por el contrario, las neuronas trabajan de forma secuencial, actualizándose sólo la salida de una neurona en cada iteración, se trata de una red secuencial o asíncrono. En este caso la salida a la que converge la red puede ser diferente en función del orden de la secuencia de activación.

B. Aprendizaje.

El mecanismo de aprendizaje utilizado es de tipo OFF LINE, por lo que existe una etapa de aprendizaje y otra de funcionamiento de la red. También utiliza un aprendizaje no supervisado de tipo hebbiano, de tal forma que el peso de una conexión entre una neurona i y otra j se obtiene mediante el producto de los componentes  y  del vector que representa la información o patrón que debe almacenar.

Utilizando una notación matricial, para representar los pesos de la red se puede utilizar una matriz de dimensión  (recordemos que N es el número de neuronas de la red y por tanto de componentes del vector de entrada). Esta matriz es simétrica () y con la diagonal con valores nulos () al no haber conexiones autorecurrentes.

También tenemos M entradas que la red debe aprender, expresadas igualmente en forma matricial, .

Utilizando esta notación, el aprendizaje consistiría en la creación de la matriz de pesos W a partir de los M vectores de entrada que se enseñan a la red.

(5.30)

Donde:
Sum_K=1,...,N:Es la sumatoria para k igual a 1 hasta el número de neuronas, N.
T(E_k): Es la transpuesta de la matriz
I :Es la matriz identidad que anula los pesos de las conexiones auto recurrentes

C. La Función de Energía.

La elección de esta regla de aprendizaje por Hopfield fue, entre otras razones, debido a que asegura la estabilidad de la red; es decir, la convergencia hacia una respuesta estable cuando se presenta una información  de entrada.

Muchas de las investigaciones acerca  de la estabilidad de las redes se basan en el establecimiento de una función, denominada función de energía de la red, para representar los posibles estados (puntos de equilibrio) de la red.

A función de energía de una red Hopfield discreta tiene la siguiente forma:

(5.31)

Donde:
: Peso de la conexión entre la neurona i y j.
: Valor de salida de la neurona i.
: Valor de salida de la neurona j.
: Umbral de la función de activación de la neurona i.

Esta expresión guarda una similitud formal con la energía mecánica clásica. Trata de representar la evolución del sistema, considerando cada configuración (vector) de las salidas de las neuronas de la red como puntos en un espacio de dimensión N y relacionando el estado de la red en cada momento con un punto de ese espacio. La función de energía puede imaginarse como una superficie que presenta determinados valores mínimos, algo semejante a un paisaje montañoso donde los mínimos serían los valles. Cuando en una red se almacenan M informaciones o patrones, los posibles estados de la red serán también M (durante su funcionamiento podrá responder ante una entrada con una salida que represente alguno de esos M patrones registrados). Estos M estados corresponden precisamente a los mínimos de la función de energía. Cuando se presenta a la entrada de la red una nueva información, ésta evoluciona hasta alcanzar un mínimo de la función energía, generando una salida estable.

Cuando la red de Hopfield se utiliza  como memoria asociativa, el objetivo es conseguir que los patrones que debe memorizar se sitúen en los mínimos de la función y, consecuentemente, sean los estados estacionarios (estables) de la red. Esto se consigue si se verifica que los pesos de las conexiones auto recurrentes son nulos (W_ij=0) y si el resto cumple la regla de Hebb (), de ahí que Hopfield eligiera dicho aprendizaje.

En cuanto a las redes de Hopfield continuas, una posible expresión de su función de energía es la siguiente:

(5.32)

Donde f^-1 es la inversa de la función de activación sigmoidal (f) de una neurona.