En cuanto a las aplicaciones más conocidas de este modelo destacan las relacionadas con el reconocimiento de imágenes y de voz, el control de motores y sobre todo la resolución de problemas de optimización. En este último ámbito se ha aplicado para la resolución de ecuaciones y del problema del viajante de comercio, manipulación de grafos, procesado de señales (conversores analógico-digitales) y de imágenes, etc.

A modo de ejemplo y para que sirva como orientación de como se resuelve un problema mediante el modelo de Hopfield, desarrollaremos a continuación el problema del vendedor viajero.

Problema del vendedor viajero (TSP: Travelling Salesman Problem)

Este problema consiste en, dadas N ciudades que tiene que visitar un vendedor, encontrar el camino más corto para, partiendo de una de ellas, visitarlas todas sin pasar más de una vez por cada una y volviendo finalmente a la ciudad de partida.

La complejidad reside en la enorme cantidad de posibles caminos, muchos de ellos de longitud similar. Para N ciudades, el número de rutas alternativas es de N!/(2N). De esta forma, para 5 ciudades existen 12 caminos posibles; para 10 ciudades, el número de rutas es de 181.440.
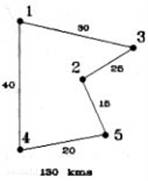
Vamos a centrarnos en el caso particular de 5 ciudades. En este ejemplo, como hemos dicho anteriormente, existirían 12 rutas cerradas diferentes, cuya longitud dependerá del orden en que se visiten las ciudades.

Distancia (en km) entre las 5 ciudades

Desarrollo

Este problema puede abordarse utilizando una red Hopfield de N*N neuronas, siendo N el número de ciudades. Aunque la red es de tipo continuo con valores en el intervalo [0,1], cuando la red se estabiliza, las salidas de las neuronas de la red tendrán valores binarios (1 si la neurona es activa). Cada neurona activa de la red informaría del orden de una ciudad determinada en el recorrido del viajero. Debemos, por tanto, imaginarnos la red como una matriz NxN donde cada fila está asociada a una ciudad, y las columnas con la posición de cada ciudad dentro del recorrido. Así, si la neurona de la fila 2 y columna 3 está activa, nos indicaría que la ciudad número 2 es la tercera en la ruta (w, x, 2, y, z).

El primer paso consiste en encontrar una expresión (bastante compleja) de la función objetivo que se quiere minimizar.

A continuación hay que relacionar esta función objetivo con la función energía de una red Hopfield para obtener una expresión, también bastante compleja, de los pesos de los enlaces de la red.

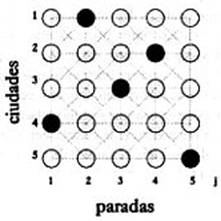
Por tanto, si se implementa una red continua de NxN neuronas con unos umbrales y unos pesos con los valores obtenidos anteriormente, se llegará a una situación de estabilidad en la que sólo habrá activa una neurona por cada fila y columna.

Para este ejemplo, la Fig. 5.3 representa la situación final de la red cuya longitud total es de 130 km.

Figura 5.3 Situación final de la red del Ejemplo. En negro las neuronas activadas.