Ejemplo 1.
Se tiene una red de Hopfield con 5 nodos y se quiere reconocer el patrón:

Puesto que la red tiene 5 nodos, se requiere de una matriz de 5*5 pesos, donde los pesos de un nodo que regresa a si mismo son cero. La matriz de pesos sería entonces:

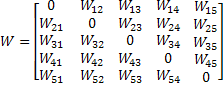
Para almacenar el conjunto de estados (patrones) .

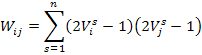
Puesto que se trata de un solo patrón, la expresión se reduce:

Puesto que los pesos son simétricos, sólo se tiene que calcular la diagonal superior de los pesos y entonces copiar a cada peso su peso específico en la matriz.

En este caso, V es el vector  , entonces:

a) Calcule  la matriz de pesos

De esta forma la matriz quedaría:

Haciendo el espejo de la diagonal, se obtiene la matriz completa:

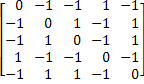
b) n=Wp1

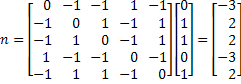
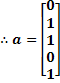
c) Dibuje la red neuronal

Ejemplo 2.
Para una red de Hopfield de 5 nodos. Se desea reconocer a los patrones:

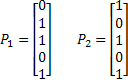
Puesto que la red tiene 5 neuronas, se requiere de una matriz de 5*5 pesos, donde los pesos de un nodo que regresa a si mismo son cero.

Para almacenar el conjunto de estados:

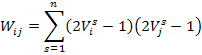
La matriz de pesos que se calculará es:

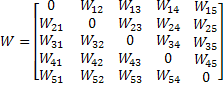
a) Calcule la matriz de pesos

Para W₁₂ la expresión es:

Donde S es el número de patrones.

De esta forma la matriz quedaría:

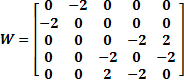
Ejemplo 3.
Considerando los datos del problema 2 y la matriz de pesos.

b) Actualice un nodo en la red de Hopfield, usando el patrón

En este caso el valor de  no cambio.

También se pudo haber calculado el producto punto de la 3ª columna de la matriz de pesos y el estado actual para calcular la suma ponderada.

a) Considerando los siguientes atractores   y .

Actualice los nodos en el siguiente orden:

3,1,5,2,4,3,1,5,2,4

En la parte a se calculo la primera actualización en el nodo 3 y no cambio.

Actualización del nodo 3
 
 
 

Actualización del nodo 5
 
 
 

Actualización del nodo 2
 
 
 

Actualización del nodo 4
 
 
 

Actualización del nodo 3

Actualización del nodo 1
 
 
 

Actualización del nodo 5
 
 
 

Actualización del nodo 2
 
 
 

Actualización del nodo 4
 
 
 

Como ya se ha actualizado cada nodo sin que ocurra algún cambio; entonces el proceso puede obtenerse.

La red de Hopfield se detuvo en el atractor