Redes Neuronales Multicapa Con Aprendizaje Supervisado
Cada capa de la red es caracterizada por la matriz de parámetros, y el funcionamiento de la red por una composición no lineal de operaciones como se muestra:
|
|
|
Una red neuronal hacia adelante (feedforward) con dos capas (una oculta y una de salida) es comúnmente usada para aproximación de mapas no conocidos. Si la capa de salida es lineal, la red puede tener una estructura similar a una red de base radial (RBF).
El Perceptrón multicapa es comúnmente usado para aproximar mapas no lineales complejos. En general, esto es posible, dos capas son suficientes para aproximar cualquier función no lineal. Por consiguiente, estamos restringiendo nuestras consideraciones a una red de dos capas.
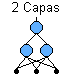
La estructura de la parte de decodificación de la red de dos capas es representada en la Fig. 3.2.
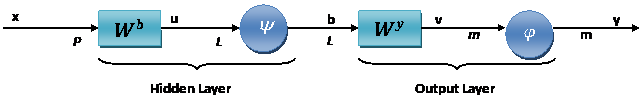
La estructura de cada capa ha sido descrita en la figura. En la capa oculta se usan funciones no lineales y en la capa de salida puede ser diferente. Existen dos matrices de pesos: una matriz de
![]() en la capa oculta, y una matriz de
en la capa oculta, y una matriz de
![]() en la capa de salida. El funcionamiento de la red puede ser descrito de la siguiente manera:
en la capa de salida. El funcionamiento de la red puede ser descrito de la siguiente manera:
|
||
|
o simplemente como:
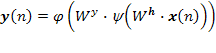 |
|
Típicamente, la función sigmoidal (tangente hiperbólica) es usada, pero existen otras funciones que también se pueden utilizar. Una condición importante desde el punto de vista del aprendizaje es que la función debe ser diferenciable.
Típicamente funciones no lineales y sus derivadas se usan en el perceptrón multicapa:
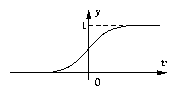
|
(3.5) |
|
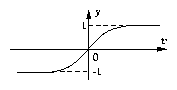
|
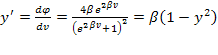 |
|
· Derivadas de la función sigmoidal son siempre no negativas.
· Derivadas pueden ser calculadas directamente desde la señal de salida usando simplemente operaciones aritméticas.
· En saturación, para valores grandes de potencial de activación, v, las derivadas se acercan al cero.
Un Perceptrón multicapa es una red con alimentación hacia delante, compuesta de varias capas de neuronas entre la entrada y la salida de la misma, esta red permite establecer regiones de decisión mucho más complejas que las de dos semiplanos, como lo hace el Perceptrón de un solo nivel.
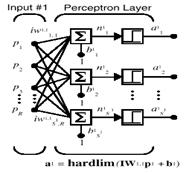
Un esquema simplificado del modelo del Perceptrón de la figura 2.1.17 se observa en la Fig. 3.3
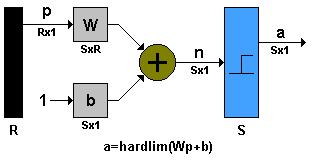
La salida de la red está dada por:
|
Donde:
![]() : Matriz de pesos asignada a cada una de las entradas de la red de dimensiones
: Matriz de pesos asignada a cada una de las entradas de la red de dimensiones
![]() , con
, con
![]() igual al número de neuronas, y
igual al número de neuronas, y
![]() la dimensión del vector de entrada
la dimensión del vector de entrada
![]() : Vector de entradas a la red de dimensiones
: Vector de entradas a la red de dimensiones
![]() .
.
![]() : Vector de ganancias de la red de dimensiones
: Vector de ganancias de la red de dimensiones
![]() .
.
Las capacidades del Perceptrón multicapa con dos y tres capas y con una única neurona en la capa de salida se muestran en la figura 32 extraída. En la segunda columna se muestra el tipo de región de decisión que se puede formar con cada una de las configuraciones, en la siguiente se indica el tipo de región que se formaría para el problema de la XOR, en las dos últimas columnas se muestran las regiones formadas para resolver el problema de clases mezcladas y las formas más generales para cada uno de los casos.
Tabla 1 Distintas formas de las regiones generadas por un Perceptrón Multicapa
Estructura |
Regiones de Decisión |
Problema |
Clases con Regiones Mezcladas |
Formas de Regiones más Generales |
|
Medio Plano Limitado por un Hiperplano |
|
|
|
|
Regiones Cerradas o Convexas |
|
|
|
|
Complejidad Arbitraria Limitada por el Número de Neuronas |
|
|
|
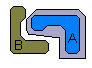
El Perceptrón básico sólo puede establecer dos regiones separadas por una frontera lineal en el espacio de entrada de los patrones; un Perceptrón con dos capas, puede formar cualquier región convexa en este espacio. Las regiones convexas se forman mediante la intersección de regiones formadas por cada neurona de la segunda capa, cada uno de estos elementos se comporta como un Perceptrón simple, activándose su salida para los patrones de un lado del hiperplano, si el valor de los pesos de las conexiones entre las neuronas de la segunda capa y una neurona del nivel de salida son todos igual a 1, y la función de salida es de tipo hardlim, la salida de la red se activará sólo si las salidas de todos los nodos de la segunda capa están activos, esto equivale a ejecutar la función lógica AND en el nodo de salida, resultando una región de decisión intersección de todos los semiplanos formados en el nivel anterior. La región de decisión resultante de la intersección será una región convexa con un número de lados a lo sumo igual al número de neuronas de la segunda capa.
A partir de este análisis surge el interrogante respecto a los criterios de selección para las neuronas de las capas ocultas de una red multicapa, este número en general debe ser lo suficientemente grande como para que se forme una región compleja que pueda resolver el problema, sin embargo no debe ser muy grande pues la estimación de los pesos puede ser no confiable para el conjunto de los patrones de entrada disponibles. Hasta el momento no hay un criterio establecido para determinar la configuración de la red y esto depende más bien de la experiencia del diseñador.
La regla de aprendizaje del Perceptrón para una red multicapa es una generalización de la regla de aprendizaje del Perceptrón simple.
| (3.10) | |
| (3.11) |
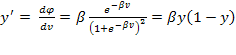 (3.6)
(3.6)