Aleatorizamos los pesos de las conexiones.

Presentamos un patrón de entrada y calculamos la salida.

Dada una unidad j-ésima de la capa de salida y unidades i-ésimas de la capa oculta inmediatamente anterior, calculamos la entrada total ponderada y la salida o activación de la misma.

Figura 3.7 Ilustra el cálculo de la capa de salida

	(3.14)
	(3.15)

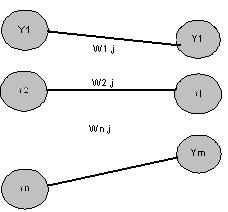Una vez computadas las actividades de todas las unidades de salida se calcula una estimación del error, generalmente una función cuadrática de los errores individuales cometidos por cada unidad, siendo cada error individual la diferencia entre la salida deseada y la obtenida.[1]

(3.16)

Siendo la salida deseada para la unidad j-ésima.

Cómputo de la rapidez de variación del error al cambiar la actividad de cada unidad de salida (EA, error respecto a la actividad)

(3.17)

Es justamente la diferencia entre la salida deseada y la salida real obtenida, es decir, la diferencia entre la actividad deseada y la actividad real.

Cómputo de la rapidez de variación del error al cambiar la entrada total que recibe cada unidad de salida.

(3.18)

Es igual a la tasa de variación del error al variar su activación multiplicado por la tasa de variación de la activación al cambiar su entrada (que es justamente la derivada de la función sigmoidal)

Cómputo de la rapidez de variación del error al ser modificado un peso de la conexión aferente a una unidad de salida.

(3.19)

Es igual a la tasa de variación del error al variar su entrada, por la tasa de variación de la entrada al variar ese  peso.

Hasta ahora sabemos calcular el EA sólo para las unidades de salida, ¿qué pasa con las unidades ocultas? En este caso no tenemos una estimación directa del error aportado por cada unidad oculta; aquí es donde interviene la retropropagación o propagación hacia atrás del error:

Figura 3.8 Propagación hacia atrás del error

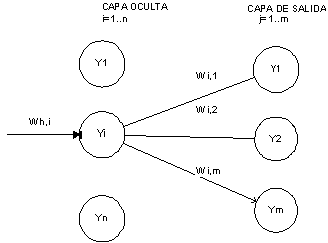
a unidad i-ésima de la capa oculta afecta a todas las unidades de salida, por lo tanto, para estimar como varía el error al variar la actividad de esa unidad oculta, habrá que sumar los efectos individuales de su actividad sobre todas las neuronas de salida. Cada efecto individual sobre la variación del  error, será igual a la tasa de variación del error de la unidad de salida al cambiar su entrada total, multiplicado por la tasa de variación de su entrada al variar  la actividad de la unidad oculta.

(3.20)

Conociendo EA para las unidades de cualquier capa podemos calcular d y EP con las expresiones ya conocidas.

(3.21)

(3.22)

Disponiendo de la tasa de variación del error respecto al peso de una conexión (EP), podemos usar distintas reglas para modificar ese peso en aras a reducir dicho de error. Una de las primeras reglas que aprovechó este algoritmo es la regla delta generalizada, que calcula el incremento a aplicar a un peso como una proporción directa de la tasa de variación del error.

(3.23)

siendo h el coeficiente de aprendizaje, típicamente con valores comprendidos entre 0.01 y 1.0

(3.24)

El algoritmo de retropropagación presenta ciertos problemas, algunos referentes a su dudosa plausibilidad neurofisiológica, y otros referentes a ciertos aspectos computacionales, que son los que vamos a comentar aquí.

Los resultados  dependen de los valores iniciales, aleatorios, de las conexiones. Esto hace que sea conveniente entrenar varias redes con distintas valores iniciales y elegir la que mejor funcione. A veces se requiere mucho tiempo para obtener soluciones sencillas. Este problema se reduce gracias al aumento de potencia de los procesadores y al uso de nuevas tecnologías, sin embargo, el tiempo de cómputo aumenta mucho al aumentar el tamaño de la red. Si bien el volumen de cálculo es proporcional al número total de conexiones. En la práctica, al aumentar el tamaño de la red, hacen falta más ejemplos de aprendizaje, y eso provoca un aumento aumenta mucho mayor del tiempo de aprendizaje. Para incrementar la velocidad de convergencia se han desarrollado diferentes modificaciones del algoritmo.

La “interferencia catastrófica” o empeoramiento en el rendimiento del sistema, como consecuencia de la incorporación de nuevos ejemplos de aprendizaje.

La parálisis: esto sucede cuando los pesos quedan ajustados a valores muy grandes, esto hace operar a las unidades de proceso con una activación muy próxima a 1, y por lo tanto, el gradiente del error tiende a 0, en consecuencia no se producen modificaciones en los pesos,  el aprendizaje queda detenido. Por eso es conveniente aleatorizar los pesos de las conexiones con valores pequeños y usar la tasa de aprendizaje, también pequeña, a pesar de que se alentase el aprendizaje.

Inestabilidad temporal. Si usamos un coeficiente de aprendizaje elevado, se van a producir incrementos grandes en los pesos, de manera que es fácil pasarse de incremento y tener que tratar de compensarlo en el siguiente ciclo, de manera que se producirían oscilaciones continuas. Esto se soluciona usando un coeficiente pequeño, o, para no tener un aprendizaje muy lento, modificar dicho coeficiente adaptativamente (aumentarlo si el error global disminuye, y disminuirlo en caso contrario).

El problema de los mínimos locales. El algoritmo de retropropagación usa una técnica por gradiente descendiente, esto significa que sigue la “superficie del error” siempre hacia abajo, hasta alcanzar un mínimo local, pero no garantiza que se alcance una solución globalmente óptima.  Sin embargo, se ha comprobado que el hecho de alcanzar mínimos locales no impide que se consigan resultados satisfactorios. Por otro lado, se han desarrollado métodos para solventar este problema, como el modo de operación asíncrona o probabilística y el uso de métodos estadísticos, como el equilibrio termodinámico simulado (ver siguiente apartado).

Figura 3.9 Problema de los Mínimos Locales

Podemos considerar el error como una superficie llena de desniveles, si soltamos una pelota caerá en algún valle, pero no necesariamente en el  más hondo, sino en el más cercano (un mínimo local). Una idea intuitiva para solucionar esto, sería aplicarle cierta energía a esa superficie agitándola o haciéndola vibrar, esto haría saltar a la pelota de valle en valle,  como de los valles más profundos es más difícil salir, tendería a estar en valles cada vez más profundos. Si dejamos de agitar esa superficie poco a poco, al final tendremos la pelota en el valle más profundo de la superficie.

Otras técnicas que pueden ayudar a no caer en mínimos locales consisten en añadir cierto nivel de ruido a las modificaciones de los pesos de las conexiones. Otra medida propuesta es añadir ruido a las conexiones, pero esto es más útil para darle robustez y aumentar la capacidad de generalización de la red. Estas medidas, por contra, aumentan el tiempo de aprendizaje.