a)  El Método del Momento
Esta modificación está basada en la observación de la última sección de la gráfica del error medio cuadrático en el proceso de convergencia típico para una red Backpropagation; este proceso puede verse en la Fig. 3.14 en la cual se nota la caída brusca del error en la iteración para la cual alcanza convergencia.

Figura 3.14 Comportamiento típico del proceso de convergencia para una red Backpropagation

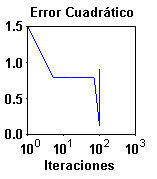
Este comportamiento puede causar oscilaciones no deseadas, por lo que es conveniente suavizar esta sección de la gráfica incorporando un filtro pasa-bajo al sistema. Para ilustrar el efecto positivo del filtro en el proceso de convergencia, se analizará el siguiente filtro de primer orden:

(3.26)

Donde  es la entrada al filtro, su salida y  es el coeficiente de momentum que está en el intervalo .

El efecto del filtro puede observase en la Fig. 3.15, en la cual se tomó como entrada al filtro la función:

(3.26)

Figura 3.15 Efecto del coeficiente de momentum

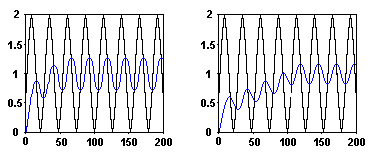
El coeficiente de momentum se asumió  para la gráfica de la izquierda y  para la gráfica de la derecha. De esta figura puede notarse como la oscilación es menor a la salida del filtro, la oscilación se reduce a medida que  se decrementa, el promedio de la salida del filtro es el mismo que el promedio de entrada al filtro aunque mientras  sea incrementado la salida del filtro será más lenta.

Recordando los parámetros de actualización empleados por el algoritmo Backpropagation tradicional:

(3.27)

(3.28)

Al adicionar el filtro con momentum a este algoritmo de actualización, se obtienen las siguientes ecuaciones que representan el algoritmo Backpropagation con momentum:

(3.29)

(3.29)

Este algoritmo, hace que la convergencia sea estable e incluso más rápida, además permite utilizar una rata de aprendizaje alta.

La Fig. 3.16 referencia el comportamiento del algoritmo con momentum en el punto de convergencia:

Figura 3.16 Trayectoria de convergencia con momentum

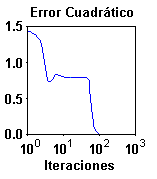
Al usar el método del momento se puede usar una velocidad de aprendizaje mayor, mientras se mantenga la estabilidad del algoritmo. El momento tiende a acelerar la convergencia cuando la trayectoria se está moviendo en una dirección constante. Este método tiende a hacer la trayectoria continua en la misma dirección.

b)  Algoritmo de Retropropagación con Razón de Aprendizaje Variable.
Este algoritmo incrementa la velocidad de convergencia incrementando la velocidad de aprendizaje en superficies planas y disminuyéndola, cuando la pendiente aumenta.

1. 1.- Si el error cuadrático se incrementa mayor a un porcentaje establecido (1% a 5%) después de haber actualizado W; entonces se descarta la actualización;
   • a se multiplica por  0 < r <  1 
   • g  se ajusta a cero (si se utiliza el momento).
2. 2.- Si el error cuadrático disminuye después de haber actualizado W, entonces la actualización es aceptada.
   • a es multiplicada por un factor h >1.
   • Si g había sido ajusta a cero, este regresa a su valor original.
3. 3.- Si el error cuadrático se incrementa en un valor menor a  z, entonces la actualización de W se acepta pero a no cambia.
   • Si g había sido ajusta a cero, este regresa a su valor original.
   • Valores típicos:  h = 1.05   r= 0.7  z=4%

La razón de aprendizaje y el tamaño del paso tienden a incrementarse cuando la trayectoria esta viajando en línea recta con una disminución del error constante. Cuando la trayectoria llega a un valle angosto la razón de aprendizaje es disminuido rápidamente. De otra forma la trayectoria se haría oscilatoria y el error se incrementaría dramáticamente.

Ejemplo:

Figura 3.17 Algoritmo de razón de aprendizaje variable