Una red RBF es no lineal si las funciones base pueden mover o cambiar de tamaño o si hay más de una capa oculta.

Las redes de base radial pueden requerir más neuronas que las redes estándar de retropropagación hacia delante, pero estas pueden ser diseñadas en una fracción de tiempo que toma entrenar a las redes hacia delante. Este tipo de redes trabajan mejor cuando muchos vectores de entrenamiento están disponibles.

Las redes de base radial constituyen la base para una transformación no lineal para un vector de entrada dado. Las funciones radiales están caracterizadas por el hecho de que su respuesta decrece (o incrementa) monótonamente con la distancia de un punto central. Una función radial típica es la función Gaussiana que, en el caso de una señal de entrada escalar, está dada por

(3.39)

Los parámetros de esta función son el centro c y el radio, denotado por s. Para el caso general de  una señal de entrada M-dimensional (vector) la función radial cambia a:

(3.40)

donde y y c son vectores de tamaño M.

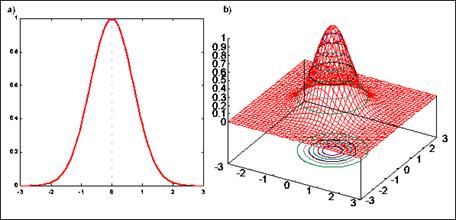
La Fig. 3.24a. ilustra una RBF Gaussiana con una señal de entrada escalar y, centro c=0 y un radio s=1. Uno puede fácilmente ver que el mencionado punto central c es simplemente el máximo de la función y que decrementa monótonamente es obvio. El decrecimiento radial característico de las RBF dado en la ecuación 1 puede ser observada al expandirse la señal de entrada en un vector de entrada de 2 dimensiones. La Fig. 3.24b muestra una gráfica de la función Gaussiana en 3 dimensiones con un vector de entrada de dos dimensiones . El centro c es un vector de la misma dimensión que la señal de entrada y y establecido en , el radio igual a uno: . La línea circular del contorno en la figura 75b ilustra que la respuesta de h(y) decrementa monótonamente incrementando la distancia de su máximo a  .

Figura 3.24 Función Radial si a) Señal de entrada escalar.    b) Vector de entrada 2-dimensional