Modelo Neuronal
La Fig. 3.21 muestra el modelo neuronal de una red de base radial con R entradas.

Figura 3.21 Modelo de una neurona de base radial

La función de transferencia, para una función de base radial es radbas. Se puede observar que la expresión para la entrada de red a una neurona con función tipo radbas no es igual a las vistas anteriormente. Una neurona con función de base radial recibe como entrada de red, la distancia vectorial entre el vector de pesos W y el de entrada P, multiplicada por el umbral B. La Fig. 3.22 muestra  gráficas de la función de transferencia de base radial.

Figura 3.22 Función de transferencia de una función de base radial

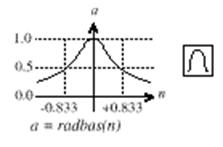
La gráfica de la Fig. 3.22 muestra una función de base radial la cual tiene un máximo de uno cuando la entrada es un cero. Esta función es útil al efectuar la resta entre el vector de pesos W y el vector de entrada. Conforme la distancia vectorial entre W y P decrece, la salida se incrementa. De esta forma  la función de base radial actúa como un detector, cuya salida es uno cuando la entrada P es idéntica  al vector W.

El umbral B permite la sensibilidad de la neurona de base radial (redbas) sea ajustada. Por ejemplo si  una neurona tiene un umbral de 0.1 este enviaría una salida de 0.5, para cualquier vector de entrada P a una distancia de 8.326 (0.8326/B) a partir del vector de peso W.

Las redes de base radial consistente de dos capas: una capa oculta de base radial (redbas) de S1 neuronas y una capa de salida lineal  (pureline) de S2 neuronas.

Figura 3.23 Arquitectura compacta de una red neuronal con funciones de base radial

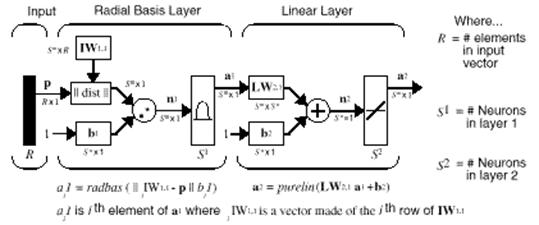
Las líneas de código contenidas debajo de cada capa de la Fig. 3.23 están contenidas en la función simurb, la cual toma un vector de entrada P, los pesos y los umbrales de la red de base radial, y regresa la salida correspondiente para cada capa.

(3.36)

Si simurb es llamado con un argumento de salida, este regresara justamente la salida de la segunda capa.

(3.37)

Se puede comprender como esta red se comporta al seguir un vector de entrada P, a través de la red a la salida a2. Si se presenta un vector de entrada tal como una red, cada neurona en la capa de base radial redbas, enviara un valor de salida de acuerdo a que tan próximo este el vector de entrada  al vector peso de cada neurona.

El resultado es que las neuronas de base radial redbas, con vectores de peso muy diferentes  de los vectores de entrada P, tendrán salidas cercanas a cero. Estas salidas de valor pequeño tendrán efectos mínimos en las salidas lineales de las neuronas.

En contraste cualquier neurona de base radial redbas cuyo vector de peso es  muy próximo al vector de entrada P tendrá un valor cercano a uno. Si una neurona tiene una salida de uno sus pesos de salida en la segunda capa pasan sus valores a las neuronas lineales pureline, en la segunda capa.

De hecho, si únicamente una neurona tiene salida uno, y todas las otras tienen salida cero o cercana a este, la salida de la capa lineal, activaría  las neuronas de los pesos de salida. Esto sería un caso extremo. Típicamente varias neuronas se activan  siempre, con variación de grados.